Lim x → 2 f(x) graph 349259-How to find the lim f(x)

Lim x!2 (x 1) (x 2) = 1 Similarly, you can show that lim x!2 (x 1) (x 2) = 1;F'(x)=1 if x>2, shown to the right f''(x)Answer lim x → ∞ f ( x) = ∞ Example 7 Use the graph below to understand lim x → ∞ x sin 2 ⁡ ( 2 x) The oscillations of this function continue to increase in amplitude, but since the function always returns to the x axis, we can't say the limit is infinite Answer lim x → ∞ x sin 2

Consider The Graph Determine The Following Limits Of The Function At X 3 Lim X Rightarrow 3 F X Lim X Rightarrow 3 F X Lim X Rightarrow 3 F X Study Com

How to find the lim f(x)

How to find the lim f(x)-X!2 f(x) (c)lim x!3 f(x) (d)lim x!4 f(x) Solution Each of these limits involves a different issue, as you may be able to tell from the graph (a)lim x!1 f(x) = 2 When x is very close to 1, the values of f(x) are very close to y = 2 In this example, it happens that f(1) = 2, but that is irrelevant for the limit The only thing that matters isSolve limits stepbystep \square!

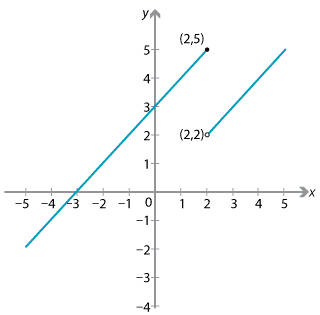
Content Limit At A Point

Lim x→0− f(x) = lim x→0 f(x) = b) Explain why the function is discontinuous at the given number a Since these limits are_____lim x→0 f(x)_____and f is therefore discontinuous at 0 c) Sketch the graph of the functionSelect a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Replace the variable x x with − 1 1 in the expression f ( − 1) = ( − 1) 2 f ( 1) = ( 1) 2 Simplify the resultMath 19, Winter 06 Homework 2 Solutions (2213) Guess the value of the limit (if it exists) lim x→2 x2 −2x x2 −x−2 by evaluating the function at the given numbers (correct to 6

Example Use the graph of y= x2 above to evaluate the following limits lim x!3 x 2 = lim x!2 x 2 = Roughly speaking, the statement lim x!a f(x) = Lmeans that as the values of xget close to (but not equal to ) a, the values of f(x) get closer and closer to L The value of the function f(x) at the point x= a, plays no role in determining theExamples 1Suppose that lim x!a f(x) = 3, lim x!a g(x) = 1, lim x !a h(x) = ¥, and lim x a h(x) = 6 Then lim x!a f(x)3g(x) = 3 3( 1) = 0 lim x!a 2f(x)g(x)h(x) = 2 3 ( 1) limFrom this very brief informal look at one limit, let's start to develop an intuitive definition of the limitWe can think of the limit of a function at a number latexa/latex as being the one real number latexL/latex that the functional values approach as the latexx/latexvalues approach latexa/latex, provided such a real number latexL/latex exists

Lim!3 f(x) = 2;Use the graph to find the limit below (if it exists) (If an answer does not exist, enter DNE) f(x) = x − 1 if x ≠ 0 −3 if x = 0 2 lim f(x) xIt#appearsthat,#asx#getscloser#and#closer#to#2#from# theleft,f(x)#getscloser#and#closer#to#05# Wesaythat*thelimit*of*f(x),*as*x*approaches*2*from*the left,*equals*05* * € x→2− limf(x)=05% Thisvalueisalsocalled"theleftFhand*limitas%x% approaches2"%

Consider The Graph Determine The Following Limits Of The Function At X 3 Lim X Rightarrow 3 F X Lim X Rightarrow 3 F X Lim X Rightarrow 3 F X Study Com

Finding Limits Using A Graph Mathbootcamps

Lim x!0 f(x) = 1;Lim x →2 f(x) = 4 An example with a function that has a jump discontinuity at x=c consisting of a single point For the function in the graph below, f(x) is defined when x = 2, but the value of f(x) at 2 is not at all similar to the value which f(x) will approach as x gets closer toLim x → 2 − f (x) = lim x → 2 f (x) = 8;

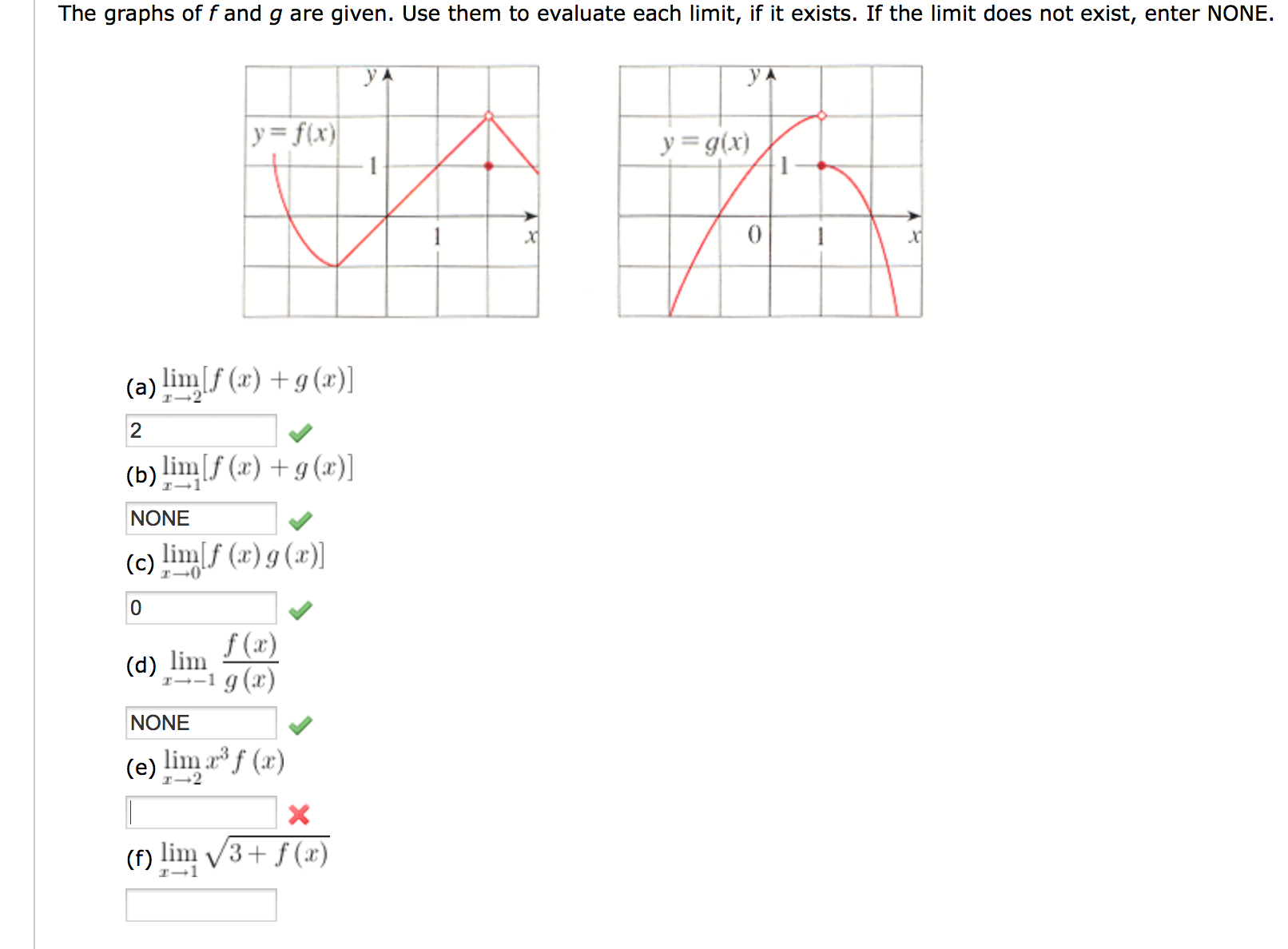
Solved The Graphs Of F And G Are Given Use Them To Evaluate Chegg Com

1

E) lim f (x) — g) lim f (x) 2 1 lim f (x) i) limf(x) exists at every c in (1, 13 Use the graph of f (x) to estimate the limits and value of the function, or explain why the limit does not exist (ii) determine lim f (x) and lim f (x) , and (iii) explain what a) lim f (x)If f(x) = x x, show that lim f(x) exists but is not equal to f(2) x2 The graph of f(x) = x > is the same as the graph of g(x) = 1 with holes at each integer, since f(a) = for any integer a Also, lim f(x) = x2 and lim f(x) = x2 , solim f(x) = X2 However, F(2) = 210 4 21 1 2 3 4 5 67 8 9 10 4 6 10 9 8 7 6 5 4 3 2 8 10 Enter your answer in the box

Limite Functions Sect22 24

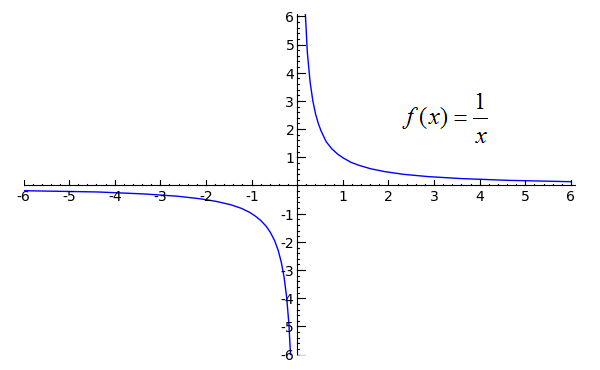
Sage Calculus Tutorial One Sided Limits

F(x) = 1 (x 2)2 f has a vertical assymptote at x = 2 So f(x) can be made arbitrarily large by choosing x values very close to to x = 2 Hence f satisfies BADLIM #1 However, by the true definition lim x!1f(x) , 1(in fact the limit is zero) This is because taking arbitrarily large values of x does not yield arbitrarily large values of f(x) ForMath131 Calculus I The Limit Laws Notes 23 I The Limit Laws Assumptions c is a constant and f x lim ( ) →x a and g x lim ( ) →x a exist Direct Substitution Property If f is a polynomial or rational function and a is in the domain of f, then = f x lim ( ) x aThe graph of a function y= f(x) is shown below Determine the following limits or state that the limit does not exist a) lim x!

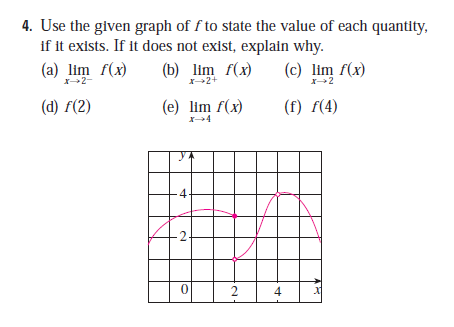
Use The Graph Of F To State The Value Of Each Quantity If It Exists If It Does Not Exist Explain Why A Lim X Gt 2 F X B Lim X Gt 2 Enotes Com

Ap Ab Exam Flashcards Quizlet

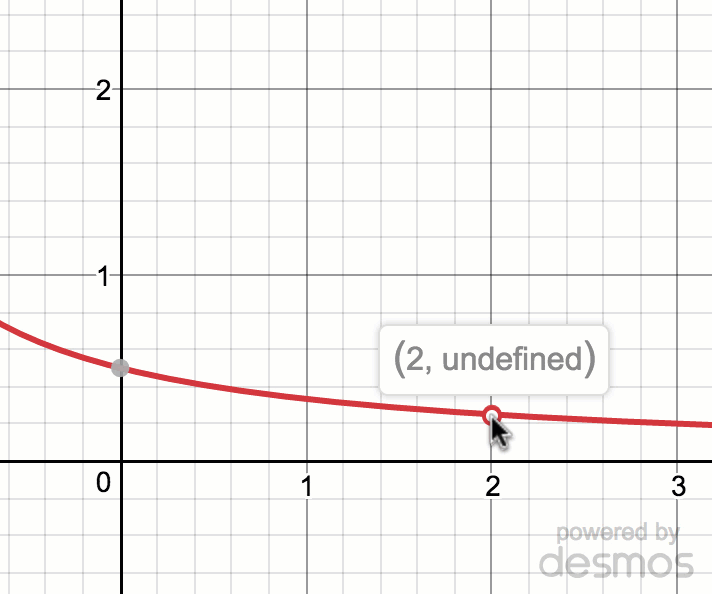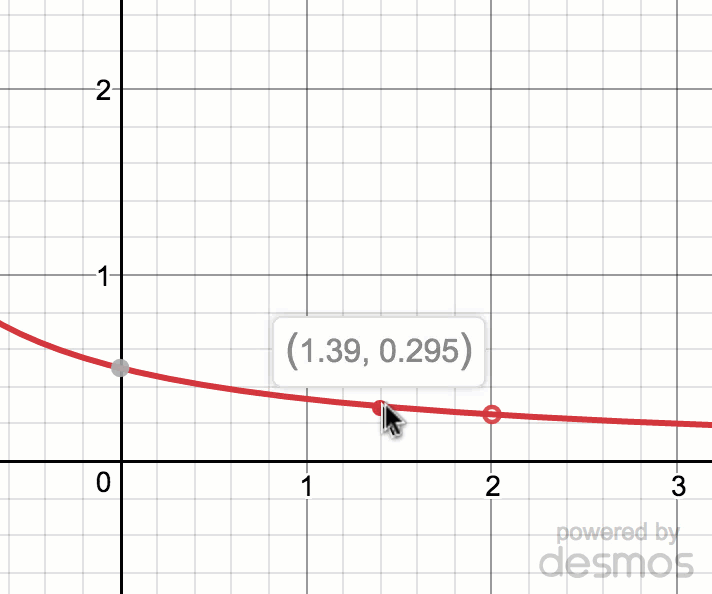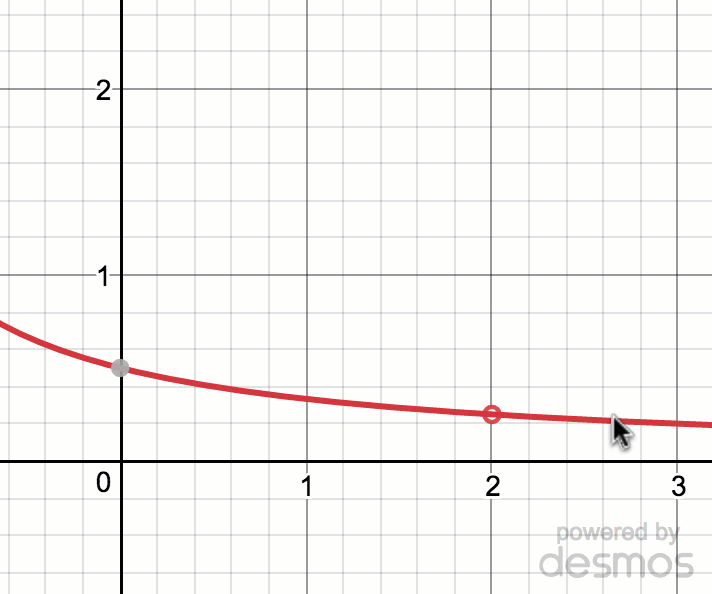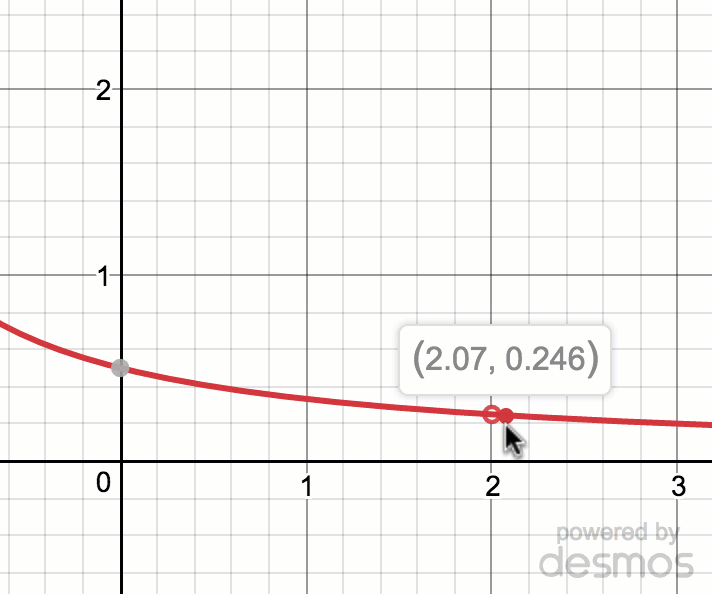
Overall Limit lim x → 2 f ( x) = 05 Let's find the limits in a couple examples Example 1 Sketch a graph and create a table to determine the limit of the function as x → 2 lim x → 2 x − 1 3 x Step 1 Graph the function Step 2 Create a table of values close to and on either side of 2 xUse the graph of f(x) to determine the value of {eq}lim x rightarrow 2 f(x){/eq} if it exists Limit of a function The limit of a function at a point exists if and only if the side limits at theSince the coefficient of x 4 x 4 is 2, 2, the graph of f (x) = 2 x 4 f (x) = 2 x 4 is a vertical stretch of the graph of y = x 4 y = x 4 Therefore, lim x → ∞ 2 x 4 = ∞ lim x → ∞ 2 x 4 = ∞ and lim x → − ∞ 2 x 4 = ∞ lim x → − ∞ 2 x 4 = ∞

Answer In Calculus For Moreen

Business Calculus

2 is an asymptote for the graph of the function fProblem 2 For the function f(t) graphed here, nd the following limits or explain why they do not exist Limits from Graphs 1 For the function g(x) graphed here, find the following limits orSelect the correct choice below and fill in any answer boxes in your choice OA lim 1x) O B The limit does not exit

Estimating Limit Values With Graphs

Does The Limit As X Approaches 0 Of The Function 1 X 2 Exist It S My Understanding That It Is Not Continuous But Both The Left And Right Hand Limits Approach Infinity Quora

When x = 2, f(x) that is the value of y will be 6 Hence the picture given above is the required graph of the statements given Question 2 Sketch the graph of a function f that satisfies the given values f(2) = 0 f(2) = 0 lim x > 2 f(x) = 0 lim x > 2 f(x) does not(a) Use a graph of f(x)=!G(x) d) lim x→0 g(x) e) lim x→2 g(x) f) equations of the asymptotes Example Sketch the graph of an example of a function f that satisfies all of the following conditions a) lim x→2 f(x) = −∞ b) lim x→∞ f(x) = ∞ c) lim x→−∞ f(x) = 0 d) lim x→0 f(x) = ∞ e) lim x→0− f(x) =

Answered Lim F X Lim F X S 2 Lim X Lim F X Bartleby

Finding Limits Using A Graph Mathbootcamps

When we get different values as x 0 approaches from left and from right, we may say that the function does not exists Question 1 Use the graph to find the limits (if it exists) If the limitUse the graph to estimate lim x → − 3 f ( x) Step 1 Examine the limit from the left Step 2 Examine the limit from the right Step 3 The onesided limits are the same, so the limit exists Answer lim x → − 3 f ( x) ≈ 2 Example 3To the pictured graph of the function y= f(x)on the interval 2,12 (a) (2 points) lim x→7 f(x)− f(7) x−7 = (b) (2 points) lim x→2 f′(x)= (c) (2 points) lim x→2 f′′(x)= (d) (2 points) lim x→2 f(x) x = (e) (2 points) Circle the smallest number in this list f

Cda Mrs Umn Edu

The Graphs Of F And G Are Given Use Them To Evaluate Each Limit If It Exists If An Answer Does Not Exist Enter Dne Wyzant Ask An Expert

X y Graph of f Graph of g The graphs of functions f and g are shown above Evaluate each limit using the graphs provided Show the computations that lead to your answer (a) 1 lim ( ) 4 x fx (c) 2 lim ( ) ( ) x f xgx (b) 3 5 lim x gx() (d) 3 lim x 1 f x gx (Assume that f and gGraph of f(x) If there are none, say so Solution f(x) = x(x 2) (x1)(x 2) = x (x1) (1) x1 = 0 =) x = 1 is a vertical asymptote (2) Verify lim x→−1 f(x) = lim x→−1 x x1 = 1 (3) (b) By calculating relevant limits, determine the equations of all horizontal asymptotes of the graph of f(x) If there are none, say so Solution lim x→∞ f(x) = lim x→∞ x x1 = limCube root of x^2 80 Evaluate the Integral integral of cos(x) with respect to x 81 Evaluate the Integral integral of e^(x^2) with respect to x Find the Derivative d/d@VAR f(x)=x^3 Evaluate the Integral integral from 0 to 10 of 4x^27 with respect to x 84 Evaluate the Integral integral of ( natural log of x)^2 with respect

The Graphs Of F And G Are Given Use Them To Evaluate Each Limit If It Exists Lim X To 2 Left X 2f X Right F 1 Lim X To 1 G X Study Com

Web Ma Utexas Edu

Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!F(3) = 1 Example 5 Use a table of values to estimate the value of the limit lim x!0 sin(x) sin(2x) (Note can us calculator to generate table) Example 6 Use the graph of the function f to state value of each limit, if it exists f(x) = 3 1 e1=x (i)lim x!0 f(x) (ii)lim x!0 f(x) (iii)lim x!0 f(x)1 f(x) = 1 b) lim x!

One Sided Limit Wikipedia

Estimating Limit Values From Graphs Article Khan Academy

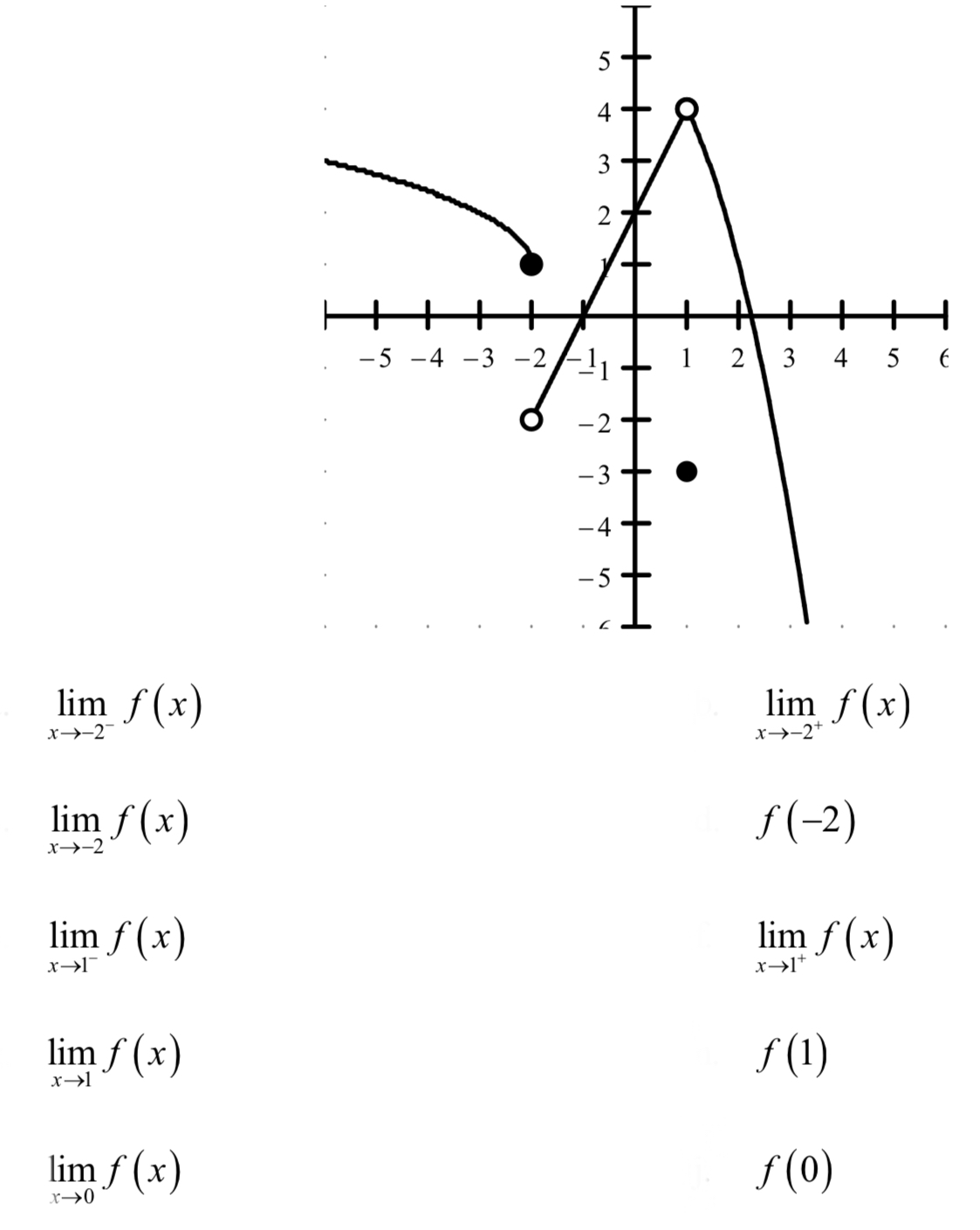
 Section 22 The Limit In the previous section we looked at a couple of problems and in both problems we had a function (slope in the tangent problem case and average rate of change in the rate of change problem) and we wanted to know how that function was behaving at some point \(x = a\) At this stage of the game we no longer care where the functions came fromExample 3 The graph below shows that as x approaches 1 from the left, y = f(x) approaches 2 and this can be written as lim x→1f(x) = 2 As x approaches 1 from the right, y = f(x) approaches 4 and this can be written as lim x→1 f(x) = 4 Note that theTranscribed image text Use the graph of the function to determine the following limits a) lim f(x) b) lim f(x) c) limx) d) limf(x) 5 a) What is the value of the limit?

Calculus Limits

Finding Limits Graphically

Lim x → 2 f (x) = 8 lim x → 2 f (x) = 8 because lim x → 2 − f (x) = lim x → 2 f (x) = 8;(ii) lim x>x 0 f(x) exists, and (iii) lim x>x 0 f(x) = lim x>x 0 f(x) = L How can we say the function is not exists by looking at its graph ?2 = e− 2 = f(x) and lim x→±∞ e− (−x)2 2 = 0, the graph is symmetry wrt the yaxis, and the xaxis is a horizontal asymptote • Wehave f0(x) = e−x 2 2 (−x) = −xe− x2 2 • Thus f ↑ on (−∞,0) and ↓ on (0,∞) • Atx = 0, f 0(x) = 0 Thus f(0) = e = 1 is the (only) local and absolute maximum • Fromf0(x) = −

Limits Of Combined Functions Video Khan Academy

Sausd Us

Ex 0 10 100 1000 lim 3 2 = − →∞ x x x x The limit as x → −∞ is the same The graph of the function in the limit above has a horizontal asymptote y = 0Answer to Solved The graph below is the function f(x) 5 4 3 2 2 1 53x2 3x1 to estimate the value of lim x→∞ f(x) to one decimal place1 02 04 06 08 10 12 14 16 1804 40 60 80 100 y = √ 3x2 8x 6− √ 3x2 3x 1 x y From the graph, it seems lim x→∞ √ 3x2 8x6− √ 3x2 3x1≈ 14 (b) Use a table of values of f(x) to estimate the

Limits

Find Limits Of Composition In The Graph Of F Mathematics Stack Exchange

And therefore the graph of y= (x 1) (x 2) has a vertical asymptote at x= 2 (check it out on your calculator) (3) lim x!0(1 x 1 jxj) Let f(x) = 1 x 1 jxj We write this function as a piecewise de ned function f(x) = 8 < 1 x 1 x = 0 x>0 1 x 1 x = 2 x x 0 74 Chapter 3 Differentiation 12 GU Let f (x) = 2x2 −3x −5 (a) Show that for h = 0, the slope of the secant line between the points (2, f (2)) and (2 h, f (2 h)) is equal to 2h 5(b) Use this formula to compute the slope of the secant line through the points P and Q on the graph where x = 2andx = 25 (c) Sketch a graph of fIndicate the points P and Q and the secant line passing through1 f(x) = 1 c) lim x!

Use The Graph Of Y F X To Find The Limits A Lim X To 4 F X B Lim X To 2 F X C Lim X To 1 F X D Lim X To 1 F X Study Com

Derivatives Days Ppt Download

For the graph shown, what is lim f(x)? lim x→c f '(x) g'(x) exists Then lim x→c f (x) g(x) = lim x→c f '(x) g'(x) In our example, let f (x) = 2x − 32 and g(x) = x −5 Note that f '(x) = d dx (2x −32) = d dx ((eln(2))x −32) = d dx (eln(2)⋅x − 32) = ln(2)eln(2)⋅x = ln(2) ⋅ 2x g'(x) = d dx (x − 5) = 1Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep

Day8

Finding Limits From A Graph Youtube

Answer to Sketch the graph of the function that satisfies all of the given conditions f'(x) greater than 0 if 2 less than x less than 2, f'(x)The left and righthand limits are equal f ( 2 ) = 4 f ( 2 ) = 4 because the graph of the function f f passes through the point ( 2 , f ( 2 ) ) ( 2 , f ( 2 ) ) or ( 2 , 4 )Lim x 3 f(x) = 2;

Use The Information To Sketch A Graph Of F X A Limit As X Approaches Infinity Of F X 1 B Limit As X Approaches 2 Of F X Infinity C Limit As

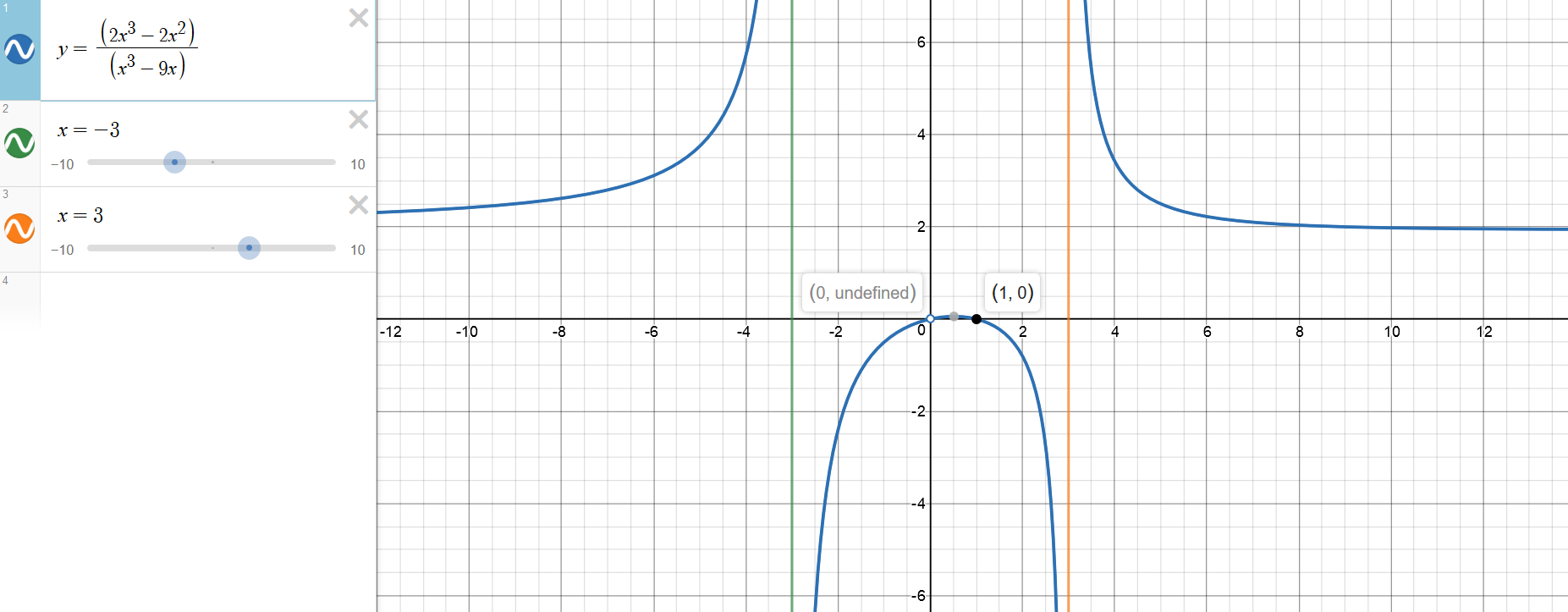
How Do You Graph F X 2x 3 2x 2 X 3 9x Using Holes Vertical And Horizontal Asymptotes X And Y Intercepts Socratic

1 f(x) =DNE d) lim x!0 f(x) = 2 e) lim x!0 f(x) = 2 f) lim x!0 f(x) = 2 g) lim x!2 f(x) = 2 h) lim x!2 f(x) = 1 i) lim x!2 f(x) =DNE 2 Evaluate the following limit usingPage 2 of 4 2 The graphs of f and g are given below Use them to evaluate each limit, if it exists If the limit does not exist, explain why (a) ( ) ( ) 2 lim x fx gx → ⎡⎤⎣⎦= (b) lim x→1 ⎡⎣2f(x)−3g(x)⎤⎦= (c) ( ) ( ) 0 lim x fxgx → ⎡⎤⎣⎦= (d) ( ) 1 ( ) lim x fx →− gx = (e) 3 ( ) 2 lim x xf x → = (f) x lim6 lim x 4 — 3x 3x — 4 2x1 3 For x 0, the horizontal line y = statements must be true?

Solved Finding Limits From A Graph Let The Graph Of The Particular Function G X Be Represented As Shown Below A Use The Graph Of G In The Figur Course Hero

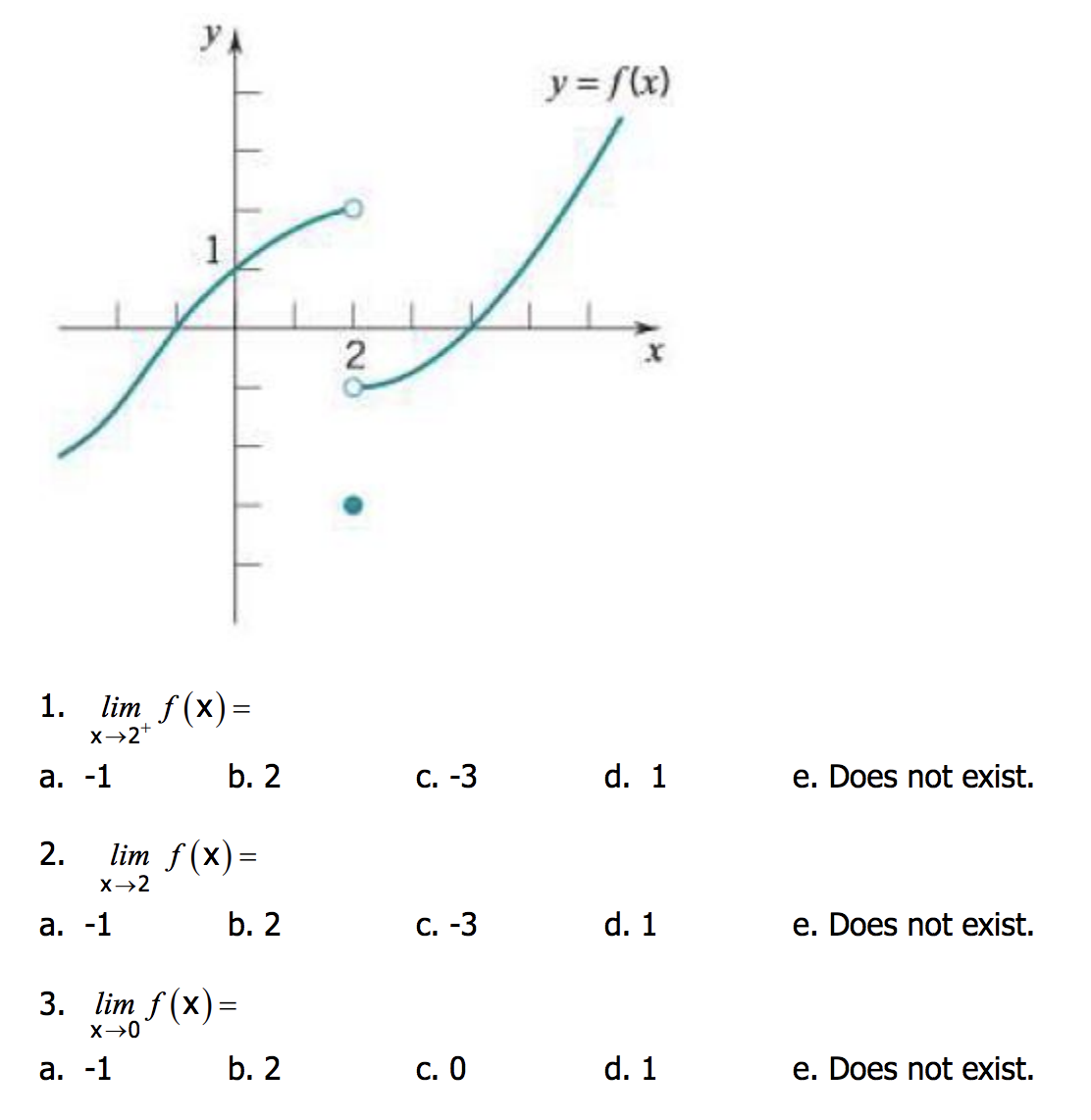
Answered 2 1 Lim F X X 2 A B 2 C D 1 E Bartleby

Suppose we are looking for the limit of the composite function f(g(x)) at x=a This limit would be equal to the value of f(L), where L is the limit of g(x) at x=a, under two conditions First, that the limit of g(x) at x=a exists (and if so, let's say it equals L) Second, that f is continuous at x=L If one of these conditions isn't met, we can't assume the limit is f(L)

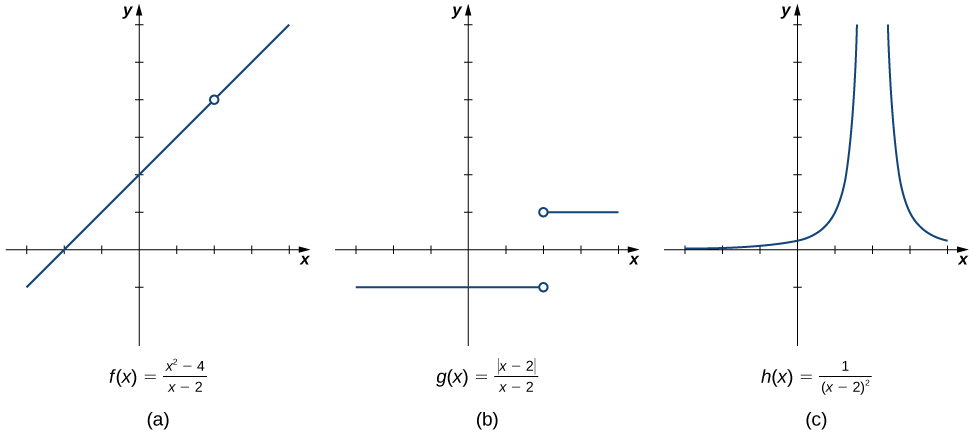
2 2 The Limit Of A Function Calculus Volume 1

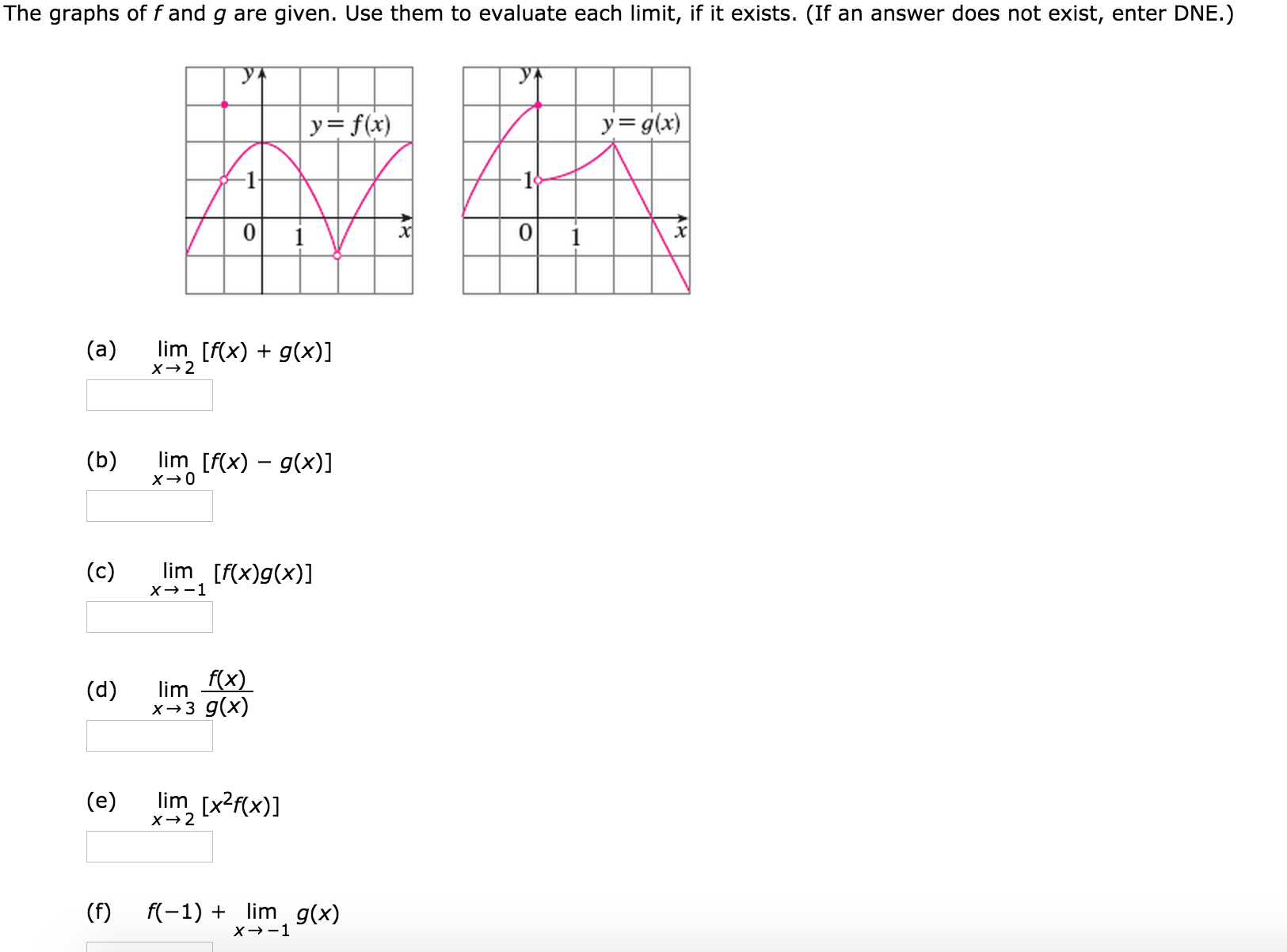
Solved The Graphs Of F And G Are Given Use Them To Evaluate Chegg Com

1

2 2 The Limit Of A Function Calculus Volume 1

12 1 Finding Limits Numerical And Graphical Approaches Mathematics Libretexts

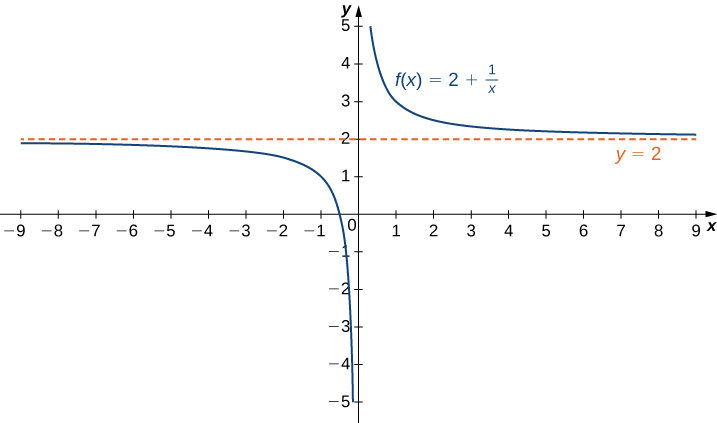
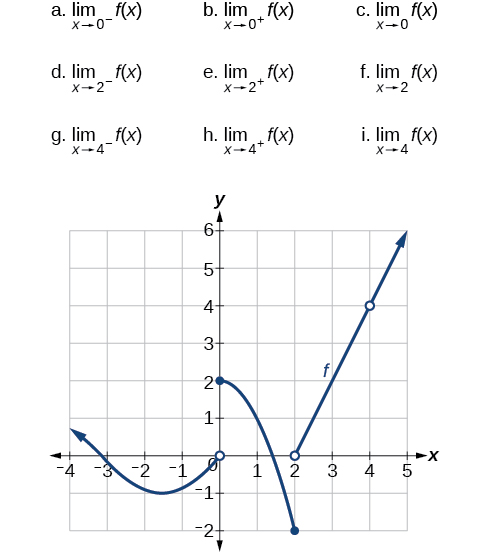
1 4 Limits At Infinity And Horizontal Asymptotes End Behavior Mathematics Libretexts

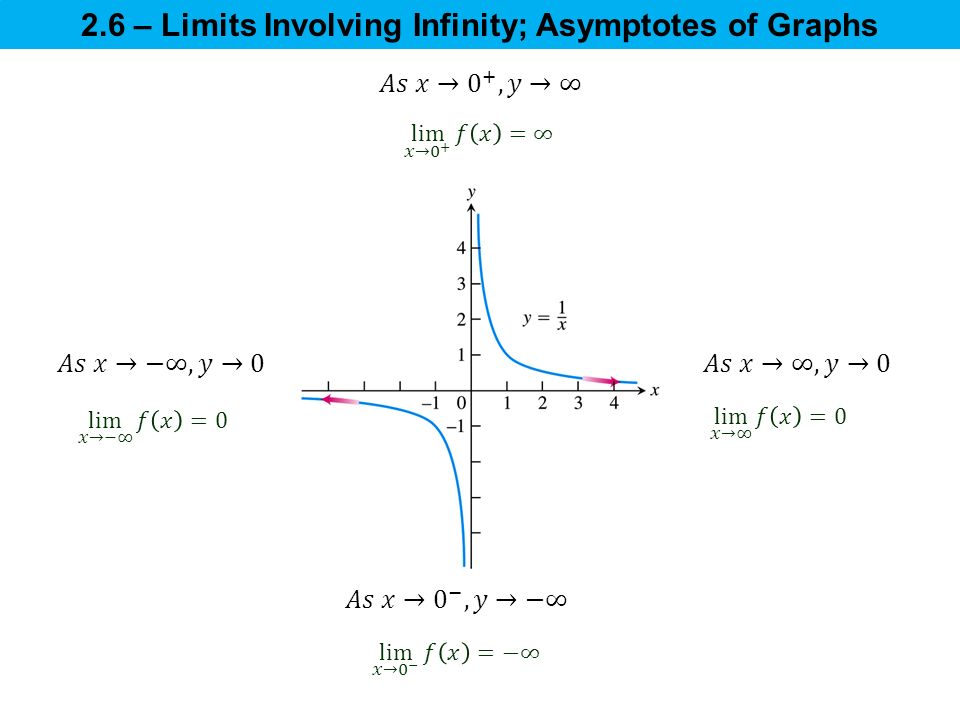
2 5 Continuity A Continuous Function Is One That Can Be Plotted Without The Plot Being Broken Is The Graph Of F X A Continuous Function On The Interval Ppt Download

1

Math 181 Quiz 1 Flashcards Quizlet

Computing Limits Graphically

Ac Using Derivatives To Evaluate Limits

The Squeeze Theorem

Calculus Limits

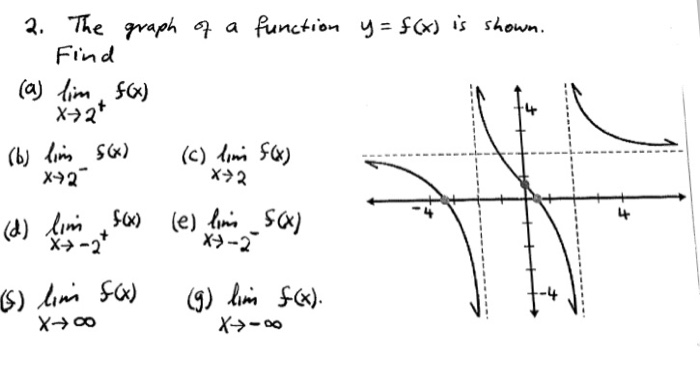
Solved The Graph A Function Y F X Is Shown Find Lim X Chegg Com

Solved Consider The Function F X Whose Graph Is Shown Below Course Hero

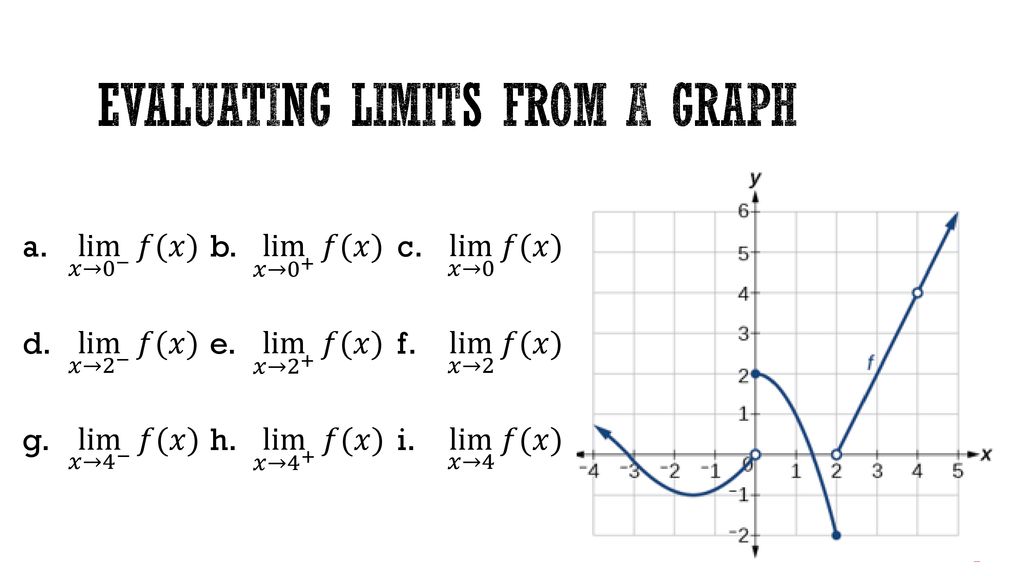
Finding Limits From Graphs Ppt Download

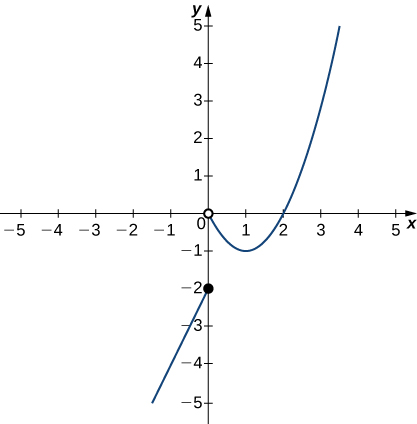
2 2 The Limit Of A Function Calculus Volume 1

Day5

If Limit X Approaches 2 Of F X 5 Then How Is It Possible That F 2 Can Be Equal To 3 Mathematics Stack Exchange

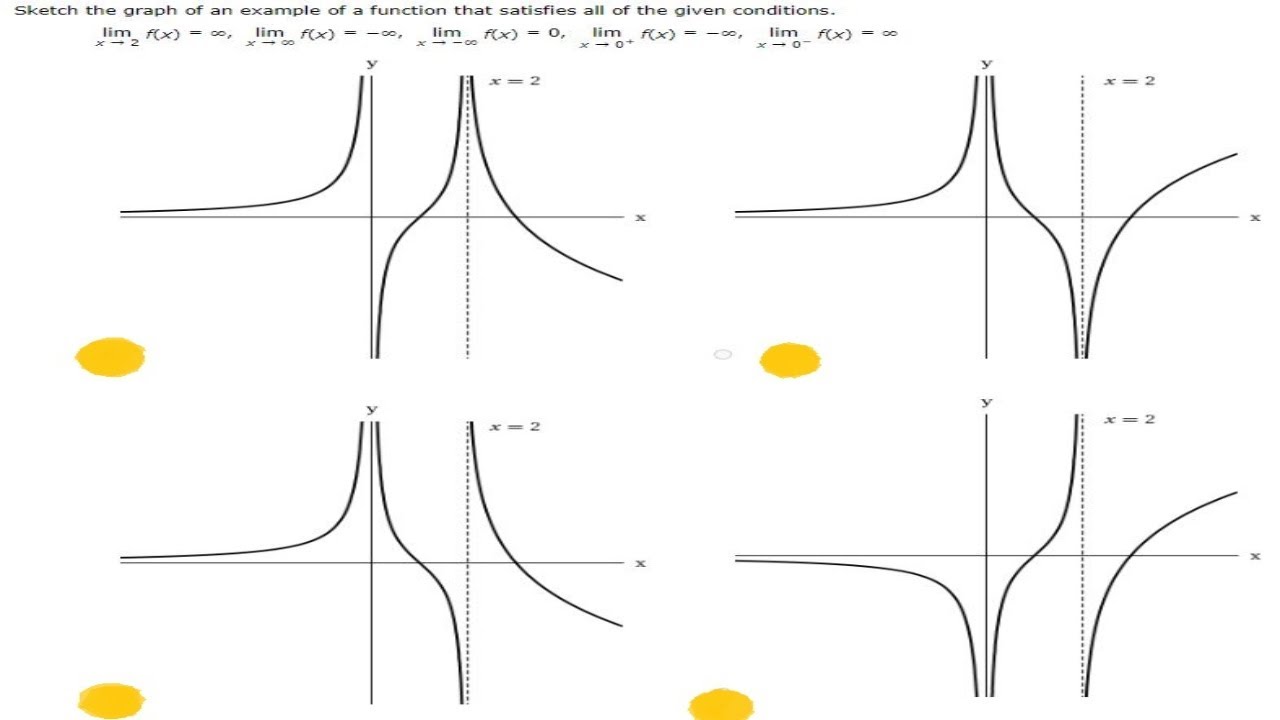
Sketch The Graph Of An Example Of A Function That Satisfies The Given Conditions Limx 2f X Youtube

Limits Introduction And One Sided Limits

Business Calculus

Use The Formula F X Lim X A F X F A X A Mathskey Com

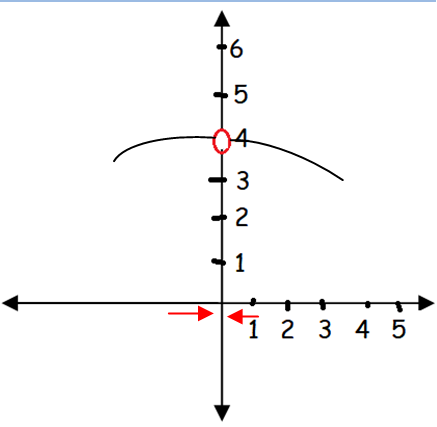
How To Sketch A Graph Of A Function With Limits

Use The Graph To Determine The Following Limits And Discuss The Continuity Of The Function At X 3 I Lim X Rightarrow 3 F X Ii Lim X Rightarrow 3 F X Iii Lim X Rightarrow

1

Ac The Notion Of Limit

Finding The Limit Free Math Help

Introduction To Limits In Calculus

Find Lim X 2 F X When Lim X 2 F X 5 X 2 3

Introduction To Limits In Calculus

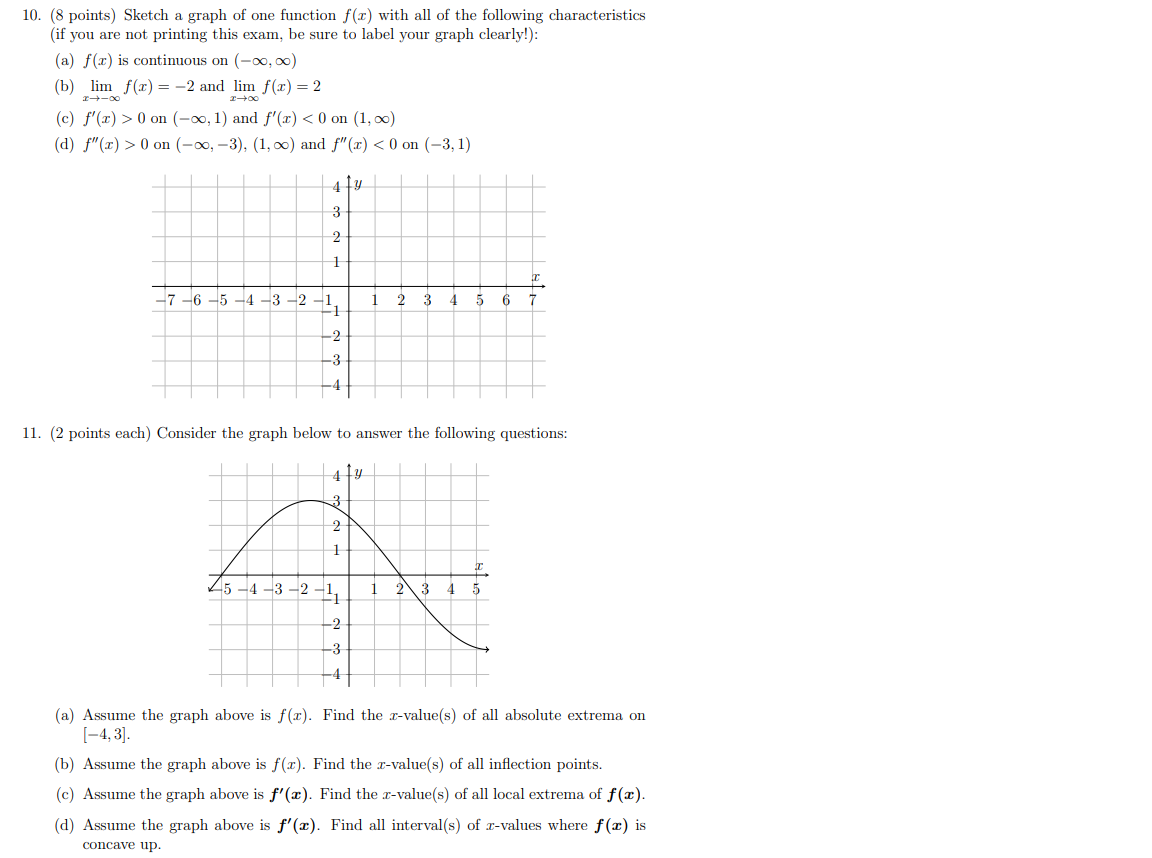
Solved 10 Sketch A Graph Of One Function F X With All Of Chegg Com

Calculus Limits

Lecture 4 Calculating Limits Using Limit Laws Click On This Symbol

Lesson 6 Limits Involving Infinity Slides

Estimating Limit Values With Graphs

Web Ma Utexas Edu

Does The Limit Exist Ap Calculus Mathematics Stack Exchange

The Graph Of The Function F Is Shown In The Figure Above The Value Of Lim X Rightarrow 0 F 1 X 2 Is A 1 B 2 C 3 D 4 E Nonexistent Study Com

Limit Of F 1 X 2 3 1 4 Or Undefined Mathematics Stack Exchange

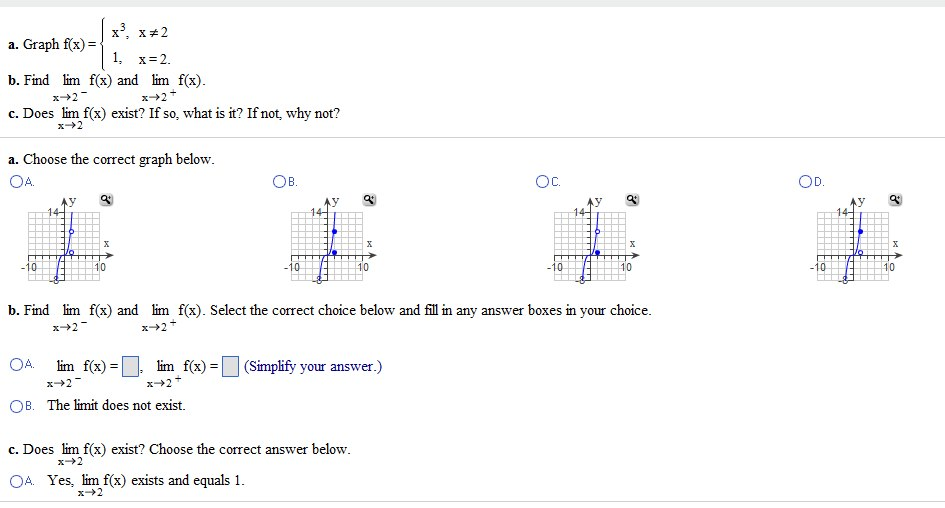
Solved Graph F X Find Lim X Rightarrow 2 F X And Lim X Chegg Com

Limits

Estimating Limit Values From Graphs Video Khan Academy

2 2 Limits Of Functions Mathematics Libretexts

2 2 The Limit Of A Function Calculus Volume 1

Limits

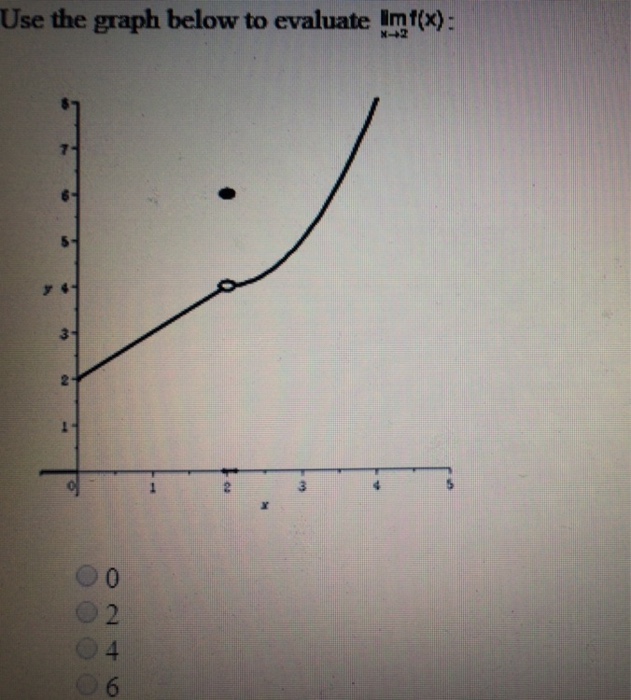
Solved Use The Graph Below To Evaluate Lim X Gt 2 F X Chegg Com

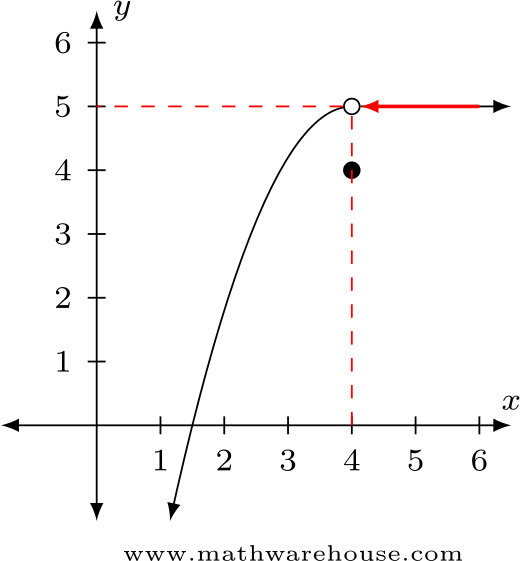
Estimating Limit Values With Graphs

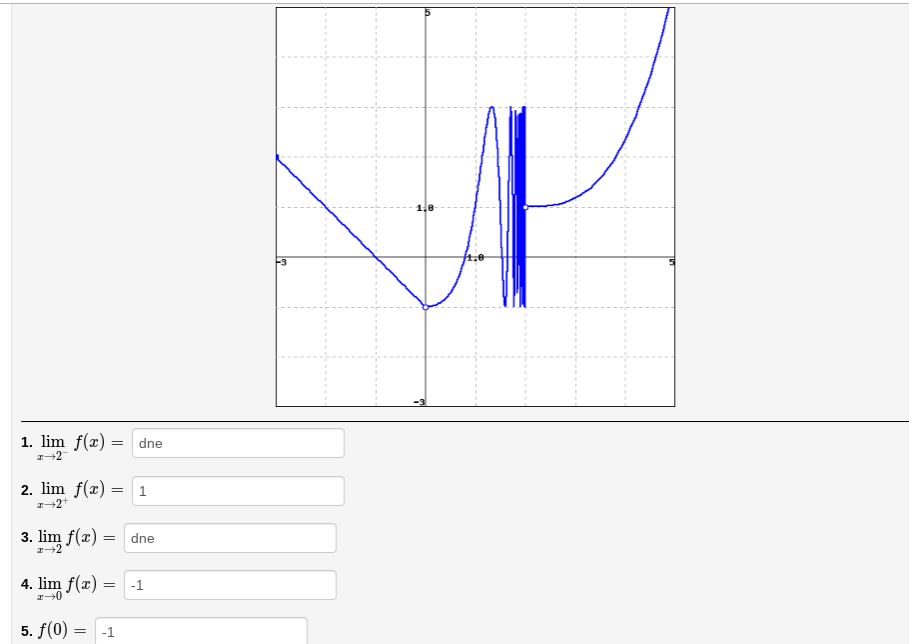
Solved Use The Given Graph Of The Function Ff To Find Chegg Com

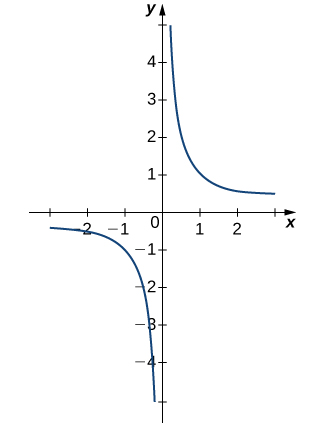
2 2 The Limit Of A Function Calculus Volume 1

Exercises Limits

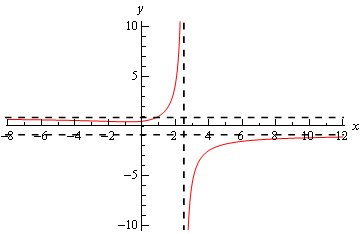
Calculus I Limits At Infinity Part I

Estimating Limit Values From Graphs Article Khan Academy

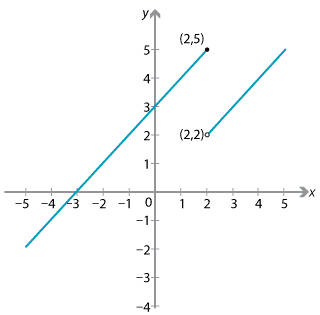
Content Limit At A Point

Finding Limits Graphically

For The Function F Whose Graph Is Given State The Following A Lim X F X B Lim X F X Youtube

Use The Given Graph To Determine The Limit If It Exists Find Limit As X Approaches Three From The Brainly Com

Limits Of Combined Functions Video Khan Academy

Does The Limit As X Approaches 0 Of The Function 1 X 2 Exist It S My Understanding That It Is Not Continuous But Both The Left And Right Hand Limits Approach Infinity Quora

Math Uh Edu

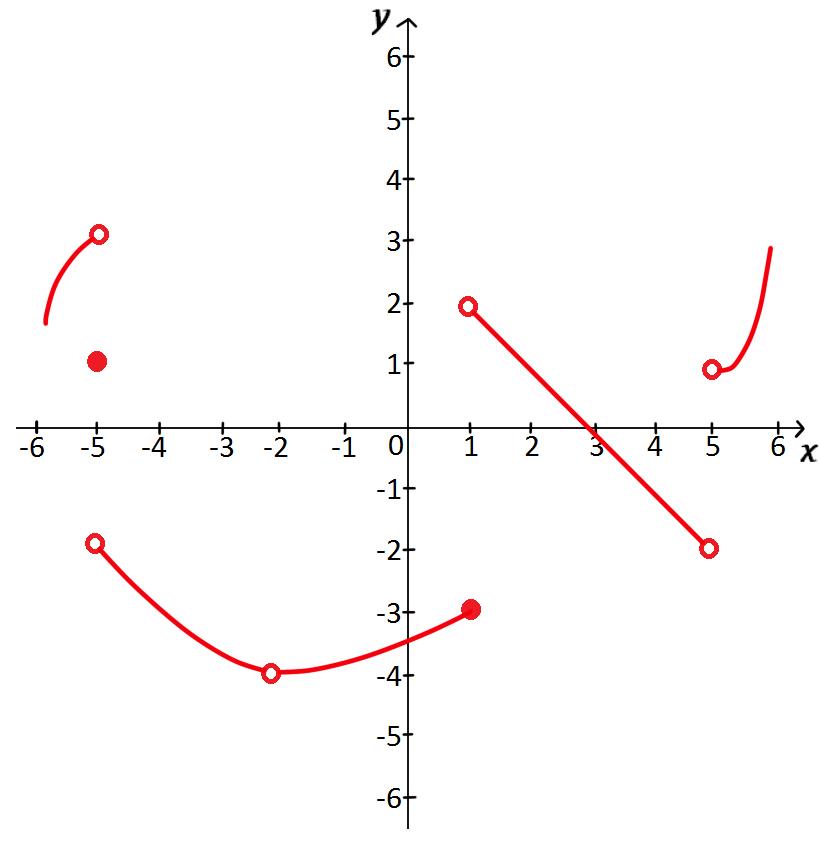
How To Find Limits From Graphs Studypug

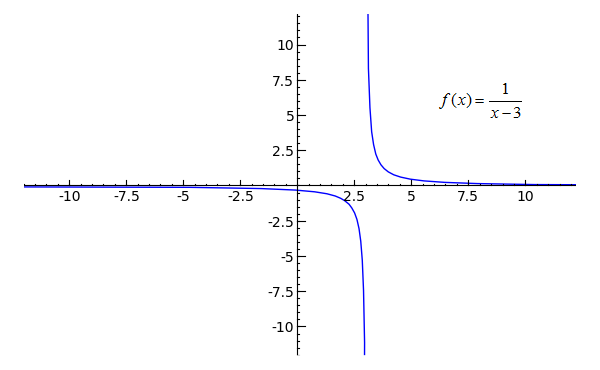
Sage Calculus Tutorial Limits At Infinity

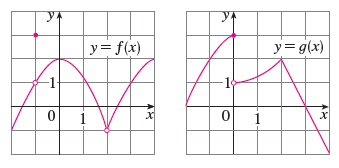
Lim X 2 F X G X B Lim X 0 F X G X C Lim X 1 F X G X D Lim X 3 F X G X E Lim X 2 X2f X F F 1 Lim X 1 G X Wyzant

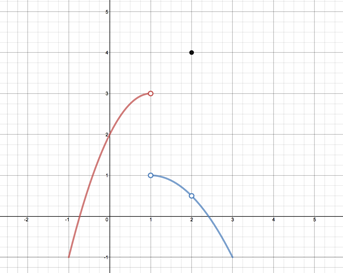
Limits Introduction And One Sided Limits

Southalabama Edu

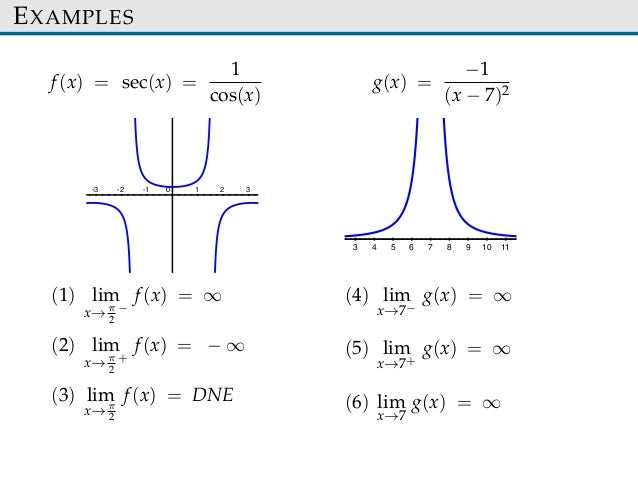
Limite Functions Sect22 24

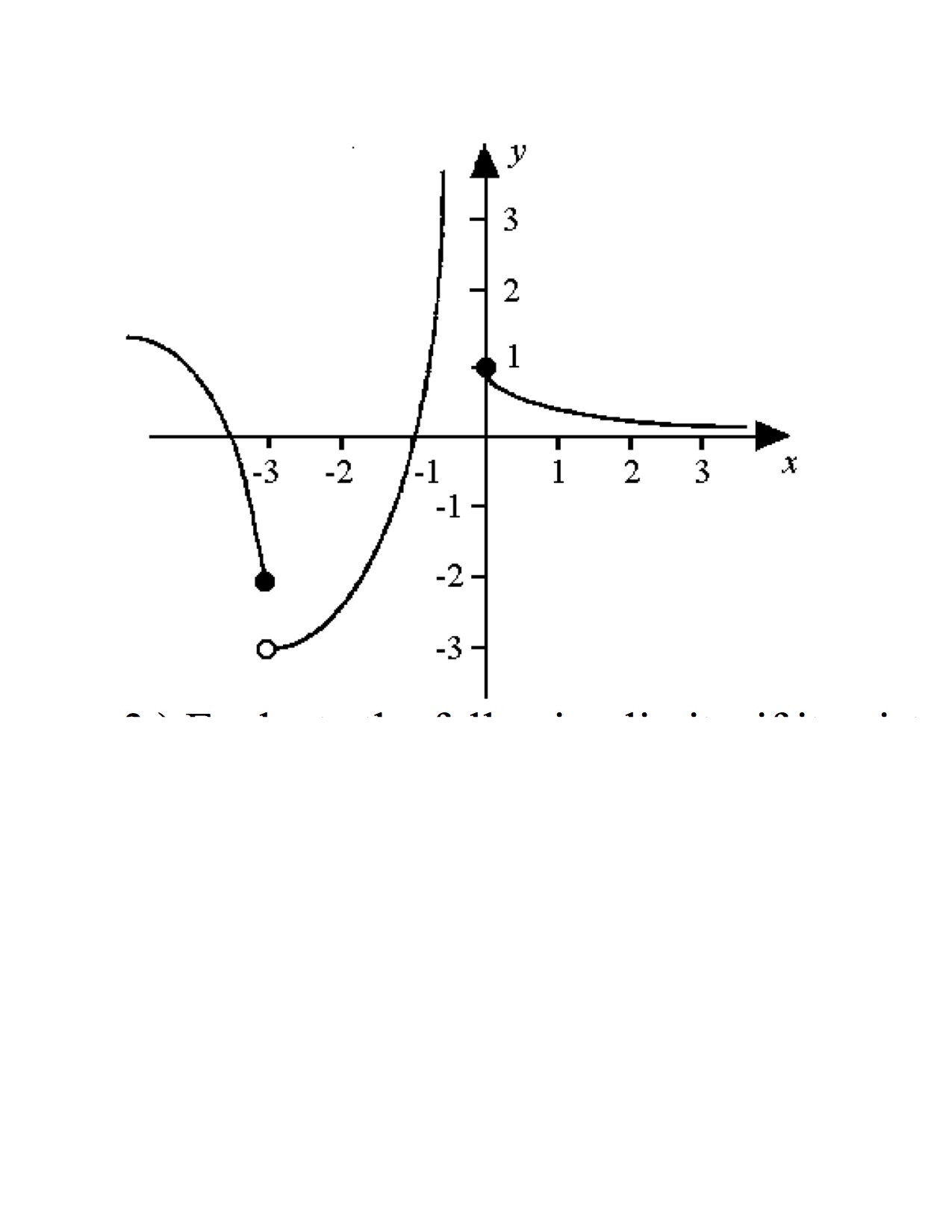
In The Following Graph How Do You Determine The Value Of C Such That Lim X C F X Exists Socratic

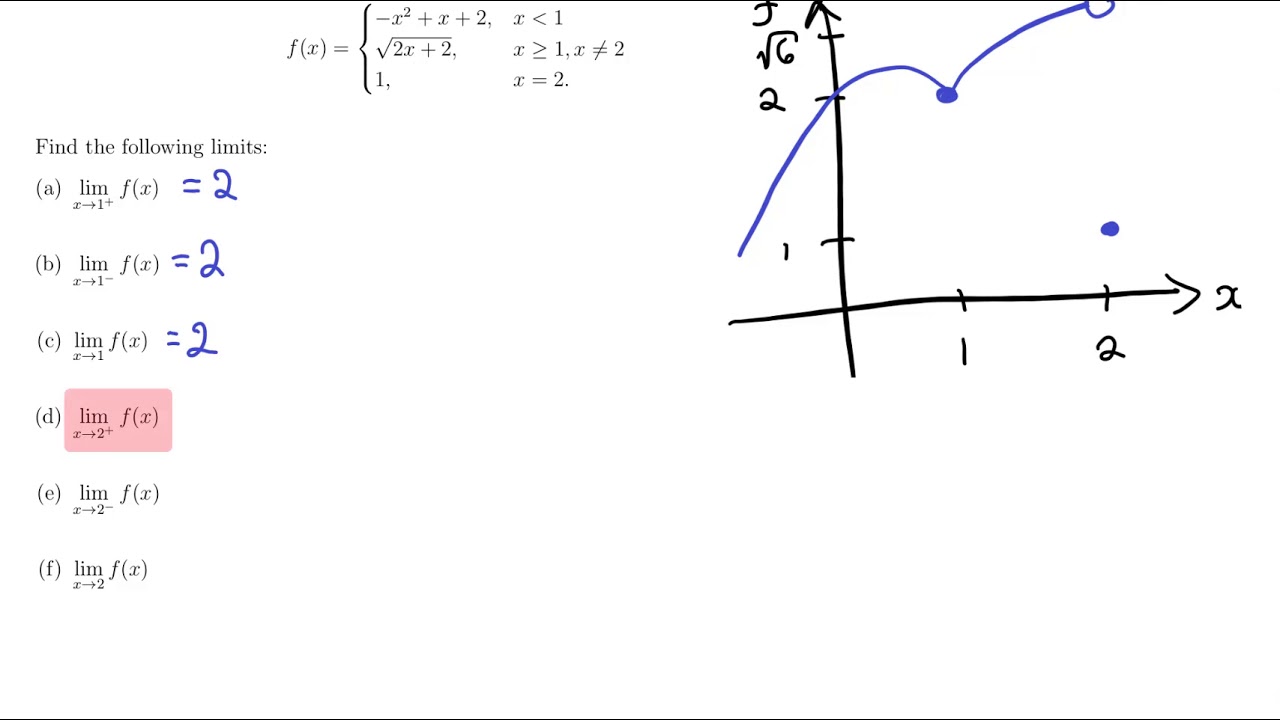
Computing Limits Graphically

Finding Limits Graphically

Evaluate Lim X 2 F X Where F X X 2 When X 2 X 2 3 When X 2 Youtube

Incoming Term: lim x → 2 f(x) graph, how to find the lim f(x),